Initial Slope by Divergence

I developed an iterative matlab algorithm in my Engineering 132 class to find the initial slope of a dataset. The algorithm quantifies the “eye test” as two numbers, divergence tolerance and error limit, then adjusts those two values iteratively until an acceptable solution is found (No, this is not gradient ascent).

How It Works

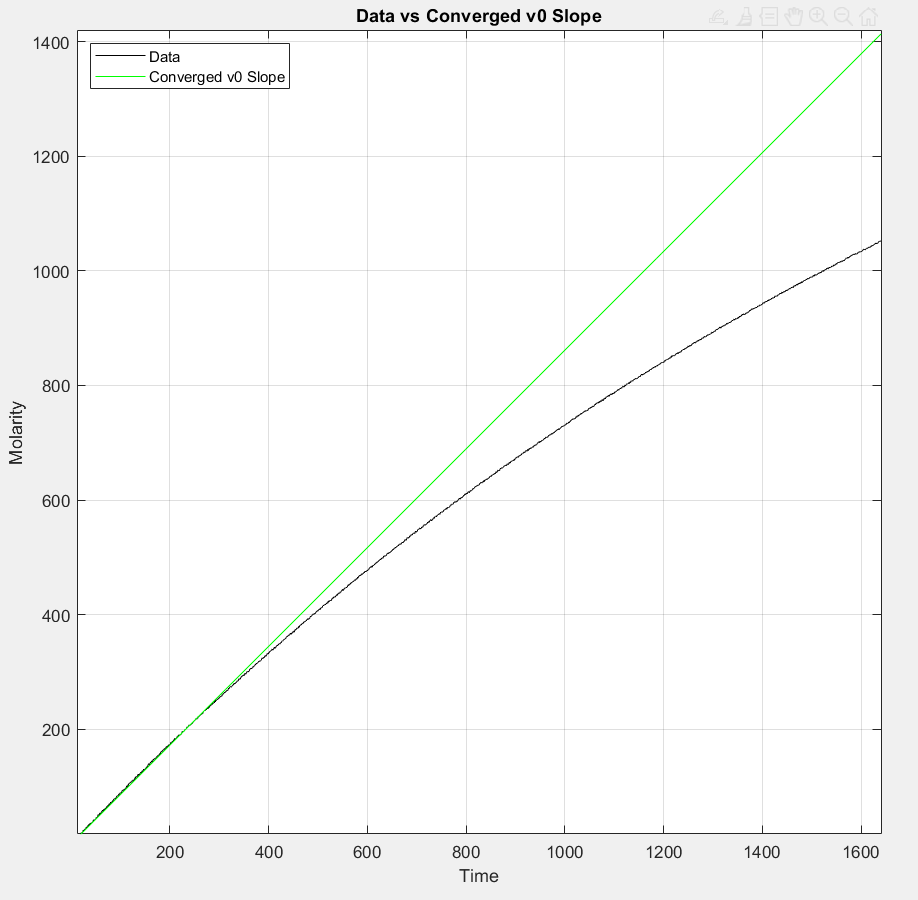
The assignment was to find the initial slope of a hundred datasets that had significant noise and outliers. All of the datasets had the same logarithmic shape, where the slope approaches infinity as time approaches 0 from the left.

My algorithm sets a “divergence tolerance” for the maximum acceptable difference of two point’s average slope with the origin. The algorithm iterates through points approaching 0 from the right, finding the difference in average slope between the current point and the previous point until it detects that the difference has exceeded the divergence tolerance.

The selected slope is then checked for error to see if it is acceptable. I defined normalized error was the average of percent squared error between the slope line and the data points to the left of the selected point, but there are a million ways to characterize error here. This method produced very consistent results without being too conservative.

If the error is below a predefined error limit, then the slope is returned as the solution. Otherwise, the algorithm continues iterating through points until it has run out of points. If this happens, it slightly increases the divergence tolerance and tries again. If, after multiple iterations, the divergence tolerance has been raised to an unacceptable amount, then it resets the divergence tolerance to its original value, and raises the error limit. By increasing these two parameters incrementally, it always returns an acceptable initial slope value.

Optimization, Noise, and Efficiency

This method reliably finds the slope with any desired level of accuracy. It is not incredibly efficient, however runtime wasn’t a constraint as long as it was reasonable (10^1 minutes), and there are a few optimizations you can make.

It only has to search the first 1/8 of the dataset, since I can assume that in this dataset, that is where all the initial slopes will be. It also can skip points. The final version compared every tenth point instead of ajacent points without noticibly affecting accuracy.

There are also a few built in ways to handle data noise and outliers. The algrithm returns the Nth acceptable solution found (I used the 20th solution) to verify that the algorithm has entered a range of acceptable solutions, and hasn’t just stumbled on an outlier. The skipping feature mentioned above also helps with noise as it also acts as sampling, and the divergence tolerance is less likely to be tripped by local variations in slope.

In future work, an optimal divergence tolerance and error limit could be finely honed by gradient ascent much more accurately and efficiently. However, linearly increasing both of those parameters was adequate to get very accurate results that greatly exceeded what was required for this assignment.